今天要來介紹的Math.hypot()是個既單純又不單純的咒語，將他唸出來看看：

「寐偲，嗨帕！」

pot在英文中是鍋子的意思，所以這感覺是一個很嗨的鍋子！

什麼情況會很嗨呢？我能想像大概就是鍋子裡頭的東西正在滾的時候，將他用鍋蓋蓋起來，鍋蓋就會不斷地跳舞，不斷地有東西想衝出來，這大概就是嗨帕的樣子吧！

圖片來源：網路

結果上網查根本不是這麼一回事。
完整的咒語請唸：

「寐偲，嗨帕托努斯！！！」

來看看什麼意思吧！

數學課

在英文中hypotenuse是「直角三角形斜邊」的意思！所以Math.hypot()的hypot指就是hypotenuse的縮寫。

雖然各位對「斜邊」的概念已經很清楚了，但還是稍微提一下吧！

我還依稀記得國中的直角三角形性質口訣：「兩股平方和等於斜邊平方。」，所以我們很清楚的知道了一個直角三角形如果知道其中兩邊的長度，第三邊就能輕鬆的推算出來了！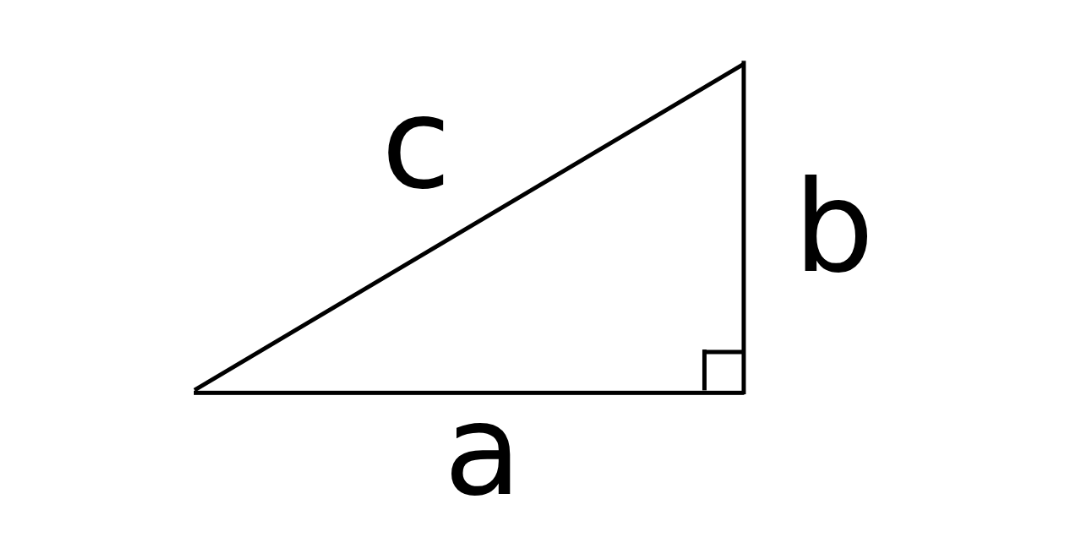

以這個直角三跟行為例，a^2 + b^2 = c^2，這就是兩股平方和等於斜邊平方。

那「斜邊」我們就可以兩邊開根號變成：c = 根號a^2 + b^2。

Math.hypot()

我們懂了斜邊如何算之後再來看看這個函式吧！

Math.hypot()會回傳參數的平方和的平方根

語法

Math.hypot()
Math.hypot(value1)
Math.hypot(value1, value2)
Math.hypot(value1, value2, ..., valueN)

參數

可以放0個到N個數字。

回傳值

他會回傳給定參數平方和的平方根，如果其中有個參數為正負無限大，那將回傳Infinity。

其中有個參數為NaN，或轉行後為NaN，將回傳NaN。

如果未給參數，或給的所有參數皆為0，將回傳0。

規範

大致上已經不需要我多做解釋了吧！
一起快速看過去：令一個空陣列...arg全部轉型後放進陣列...如果有正負無限大就回傳無限大...如果有NaN就回傳NaN...

好啦！大致上就跟剛剛講的都一樣，但最後寫道：「The "length" property of this function is 2𝔽.」

這是什麼意思呢？

其實就是Math.hypot()這個函式預期要放兩個參數，即使他可以調整參數的數量還是可以正常運作，但 ECMAScript 認為這個函式操作時最理想是放入兩個參數，而放入兩個參數正好也符合函式名稱的「斜邊」一詞。

應用

知道Math.hypot()是什麼之後就能輕易的求出直角三角形的斜邊長啦！

console.log(Math.hypot(3, 4)); //5
console.log(Math.hypot(5, 12)); //13
console.log(Math.hypot(1, Math.sqrt(3))); //2
console.log(Math.hypot(1, 1)); //1.4142135623730951(根號2)

測試了一些常見的直角三角形也沒問題！

那他還能運用在何處呢？其實在數據分析中，判斷兩個個體之間的差異有時候會使用「歐氏距離」跟「餘弦相似度」做計算，那我們就來看看這兩個可愛的東西是什麼吧！

歐幾里得空間

古希臘數學家 歐幾里得提出了幾何原理，後來被拿來整理成歐幾里得空間，用來描述生活中的空間概念。

在歐幾里得空間中最基本的單位是「點」，二維空間（平面）中我們可以定義平面上的點(x, y)；三維空間（立體）我們可以定義空間中的點(x, y, z)；到了多維的空間，雖然我們很難想像四維以上的空間，但我們可以透過對歐幾里得幾何原理的推廣來描述任意多維的歐幾里得空間，那這個空間的點就會是(x1, x2, x3, ..., xN)。

歐氏距離

直接看看維基百科的定義：

歐氏距離用來計算在歐幾里得空間中，兩個點的距離，兩個點的距離越接近，代表這兩個點越相似，不管這個點是多少維度，我們都能透過上面的d(x, y)算法來得到兩個點之間的距離，而這個算法剛好也就是Math.hypot()在做的！

const a = [1, 2, 3];
const b = [5, 2, 4];
console.log(Math.hypot(...a.map((element, index) => element - b[index]))); //4.123105625617661

這個4.12310...就是歐氏距離了！

const a = [1, 2, 3, 4, 5, 6];
const b = [1, 2, 3, 4 ,5, 6];
console.log(Math.hypot(...a.map((element, index) => element - b[index]))); //0

可以看到兩個點重合時（相似度100%）就會算出距離0！
如此一來我們就能判斷兩個資料之間的相似程度了！

餘弦相似度

計算餘弦相似度之前我們要先理解內積是什麼。

內積

因為等等會用到，我們今天就先簡單教大家一下如何計算就好，關於內積的意義，實在是一言難盡，有很多發揮空間，這有興趣的可以再去研究，。

兩向量的內積計算，我們有兩個向量(x1, y1)跟(x2, y2)，他的內積就是(x1 * x2) + (y1 * y2)。

所以(1, 2)跟(3, 4)，那這兩個向量的內積就會是1*3 + 2*4 = 11。

內積的幾何定義

透過兩個向量的內積除以兩向量的長度相乘，就能得到cos值！

計算餘弦相似度

我們可以將每筆資料都視為一個向量，假設三維空間的點(1, 2, 3)跟(1, 2, 4)，就可以得到從(0, 0, 0)指向(1, 2, 3)跟(1, 2, 4)的向量。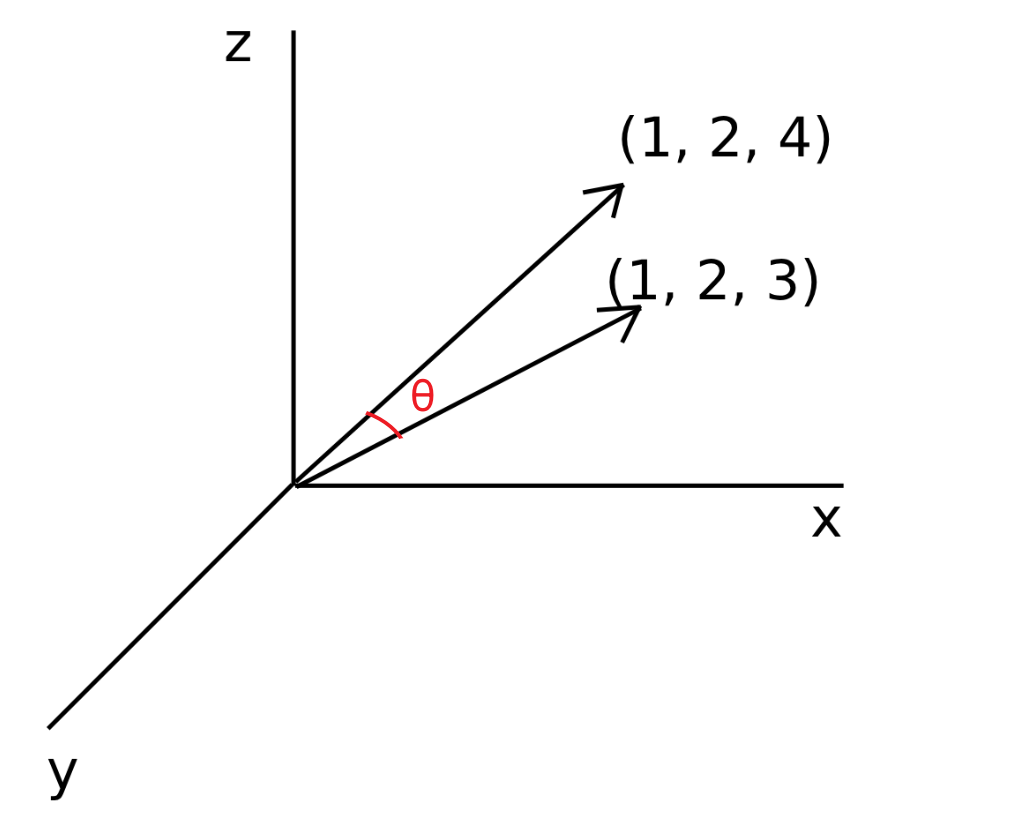

然後我們就可以使用這兩個向量去計算出它們的夾角：

const v1 = [1, 2, 3];
const v2 = [1, 2, 4];

const v1Dotv2 = v1.reduce((sum, element, index) => {
    return sum + element * v2[index]
}, 0)

const cosSimilarityBetweenV1andV2 = v1Dotv2 / (Math.hypot(...v1) * Math.hypot(...v2));
                                 
console.log(cosSimilarityBetweenV1andV2); //0.9914601339836675

喔！算出來了，這兩個向量的餘弦相似度是0.9914....，非常接近1，那如果改成兩個一樣的向量呢？

const v1 = [1, 2, 3, 4, 5];
const v2 = [1, 2, 3, 4, 5];

const v1Dotv2 = v1.reduce((sum, element, index) => {
    return sum + element * v2[index]
}, 0)

const cosSimilarityBetweenV1andV2 = v1Dotv2 / (Math.hypot(...v1) * Math.hypot(...v2));
                                 
console.log(cosSimilarityBetweenV1andV2); //1

算出的結果就是1了！

相信透過上面的例子大家已經觀察到了！餘弦值是1就代表夾角為0度角，表示這兩個向量完全貼合，那不就是代表他們完全一樣嗎～

相反的如果計算出來的夾角越大，那也表示這兩筆資料的相似程度就越小，越沒有關聯。

呀！終於講完了，在鐵人賽的倒數第二天，也就是會丟出新東西的最後一天，似乎講了非常厲害的東西呢！！！有關數據分析這類的資訊，小弟我也不是很了解，只能跟大家分享自己稍微研究出來的成果跟想法，也歡迎各位大大留言給我更多指教！

最後一次唸咒語了，大家肯定非常不捨吧！讓我們大聲唸出來讓旁邊的人都用崇拜的眼神望著你！

「寐偲，嗨帕托努斯！！！」

我們明天見！
參考資料：
MDN-Math.hypot()
ECMAScript-Math.hypot()
維基百科-歐幾里得空間
維基百科-歐幾里得距離
歐氏距離與餘弦相似度
維基百科-內積
餘弦相似性